What is the difference between the ellipsoid, mean sea level, geoid, geoid height, and orthometric height — and which one is right?
By Eos Positioning Systems
Meet Michael Smith. Michael is the (fictional) GIS analyst at an (also fictional) U.S. utility company. As such, Michael is responsible for ensuring its field technicians collect accurate asset location data, including elevations. To produce accurate (within centimeters) elevation data required, Michael is tasked with surveying the utility’s water assets in the field. He bought a new iPad mini®, installed Esri’s ArcGIS Collector, and configured a high-accuracy Arrow Gold GNSS receiver via Bluetooth to create the perfect, easy-to-use field data collection solution.
But before sending his field crew out with the technology, Michael wanted to make sure the solution worked.
So, Michael took his iPad® and Arrow Gold into the field and tested them by recording the elevation of a survey monument. A survey monument is a point with published high accuracy horizontal and vertical coordinates. In the United States, you can find information on such monuments in your area via the National Geodetic Survey (NGS) website.
Michael recorded his elevation measurement from his devices, compared it with the published coordinates, and was surprised. His GPS receiver elevation data was off by tens of meters.
Is the GPS receiver wrong?
Part 1: The “Ellipsoidal Model” — Your GPS receiver measures elevation with respect to “the ellipsoid”
Michael’s GPS receiver works just fine. But to understand why his elevation data seems wrong, we need to understand what kind of “elevation” his GPS receiver is measuring.
All elevation measurements are, in essence, the difference between the earth’s surface and a point above or below it. But because the earth’s surface is full of physical anomalies and is changing constantly, scientists rely on theoretical representations — called “vertical datums” — to represent the earth’s surface.
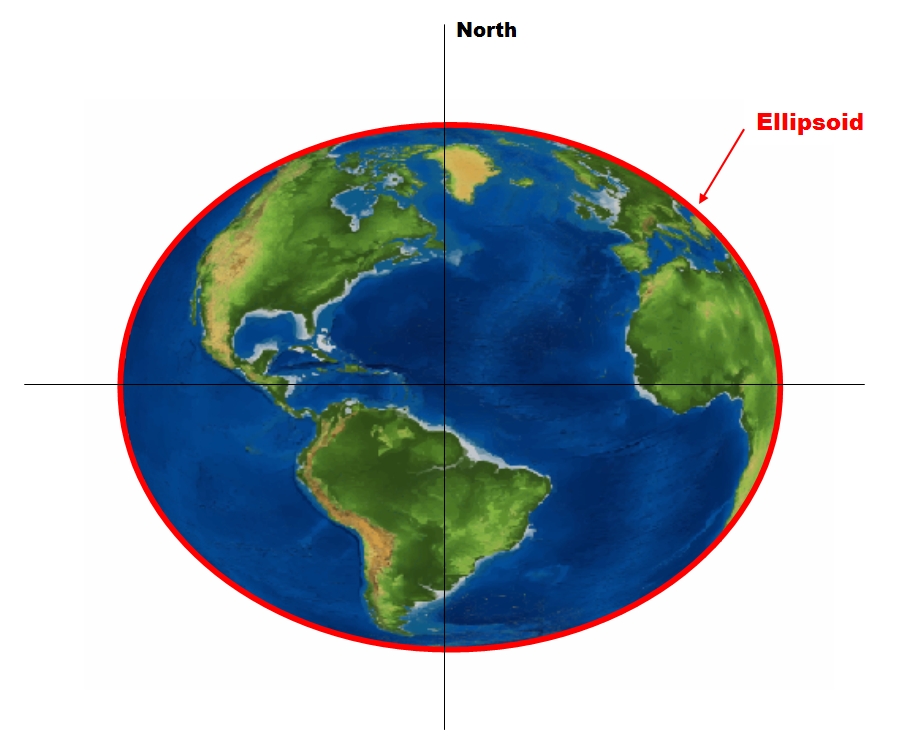
Michael’s GPS receiver is referencing a theoretical representation of the earth’s surface called the “ellipsoid.”
Recall that an “ellipsoid” is a 3D shape like a sphere, but more like an oval. The earth is shaped like this, with the north and south poles acting as the top and bottom points of an approximate egg. The ellipsoid is a mathematical conception of the earth’s surface, which is referenced by GPS / GNSS receivers like the Arrow Gold because it is extremely accurate. So, when a receiver collects elevation data, it is referenced to the ellipsoid.
However, there is a problem with ellipsoidal elevations. Although they are very accurate, they are not practical for every day operations, such as field work.
Let’s take a look at why.
The issue is that the earth is not a perfect ellipsoid. It has mountains, craters, and other features above or below the mathematically perfect ellipsoidal reference. That’s why you could take a GPS receiver on a boating dock at “sea level” and capture a — perfectly accurate — ellipsoidal height of -20 meters. But a dock isn’t 20 meters under water (or you would have bigger issues than interpreting your GPS receiver). So, although your GPS receiver’s ellipsoidal reading is accurate, it doesn’t seem to make sense.
Therefore, GIS users must transform their ellipsoidal data into a practical elevation reference.
What should I remember about ellipsoidal data?
- All elevation data is based on a defined “vertical datum”
- A vertical datum is a representation of the earth’s surface (considered to be 0 meters)
- GPS receivers measure elevation with reference to an ellipsoid
- Ellipsoidal data is accurate, but not a common elevation reference
Part 2: Mean Sea Level — What is the MSL my GPS receiver outputs? (And could I use that?)
The vertical reference often used to represent the earth’s surface called the “mean sea level,” or MSL. MSL is a local tidal datum that can be used as a reference for elevation when close to the shoreline. However, once you get more than a few kilometers inland, MSL becomes impractical. Your GPS / GNSS receiver already outputs global MSL, because MSL is a standard for position output.
MSL can be calculated two ways. First, it can be measured locally, by taking data over time about the highs and lows of ocean tides (based on the gravity of the moon, sun, earth, and other variables). And by averaging the past 19 years of these global sea highs and lows, scientists have also been able to create a global MSL, which GPS receivers sometimes used as a reference for measuring elevation.
However, it’s important to note that the global MSL on your GPS receiver is generally based on a coarse 10-minute by 10-minute grid. This can make the global MSL elevations output by GPS receivers off by several meters.
So how can you use your GPS receiver elevations for practical applications?
What should I remember about MSL?
- Mean sea level “MSL” is an elevation reference output by GPS receivers
- MSL elevations don’t take into account local factors
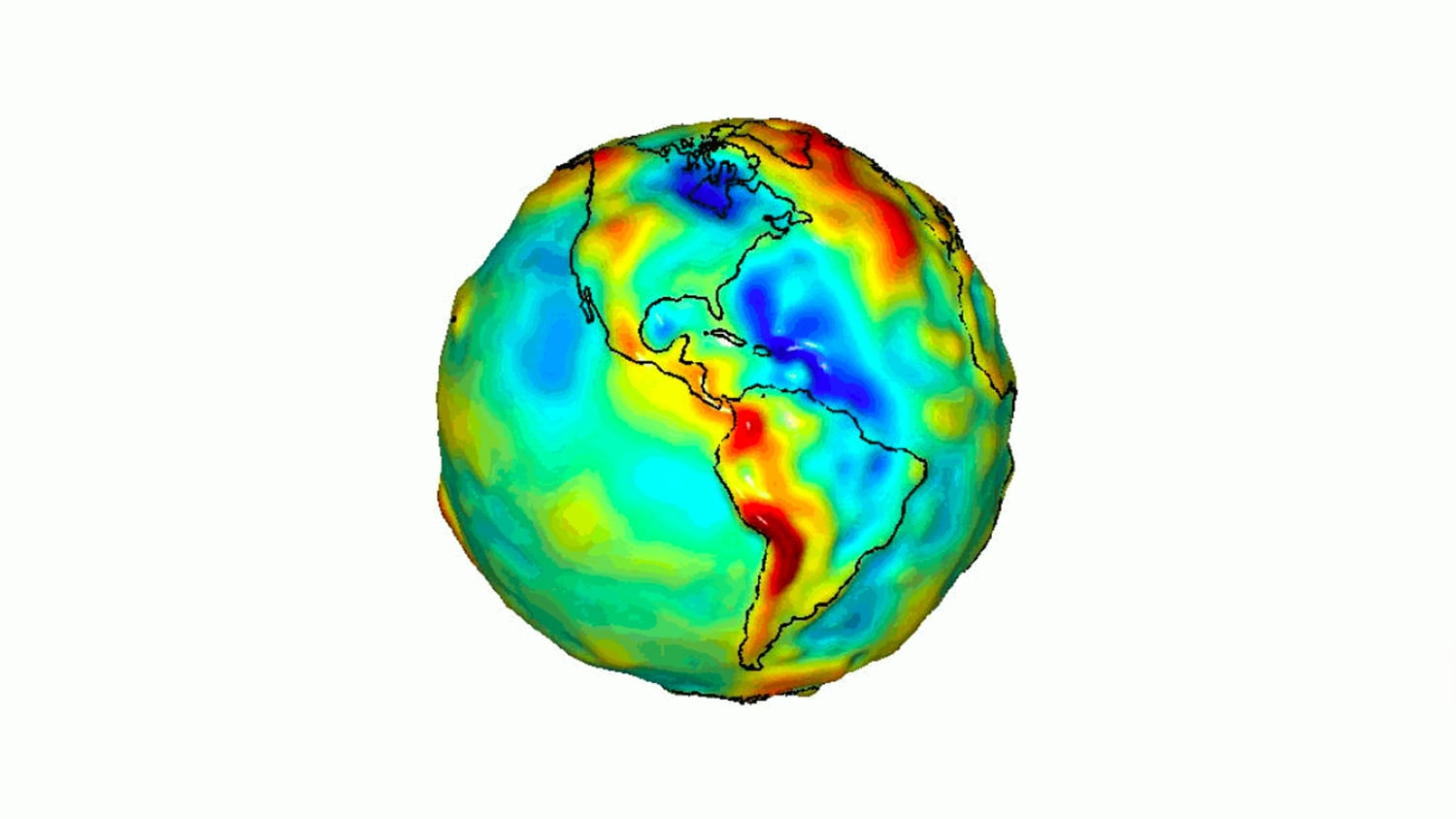
Part 3: The Geoid — A model of the Earth’s gravity field which best fits a global MSL
The geoid[/caption]
What is the geoid?
The geoid is similar to, and sometimes confused with the MSL because both are based on similar factors (such as gravitational forces). However, the geoid is far more accurate because it is a locally calculated geometric representation of the actual physical shape of the earth. For example, in the United States, the current vertical datum is called NAVD88 (North American Vertical Datum of 1988) and incorporates the latest geoid model (see below; GEOID12B).
To compute NAVD88 elevations, you’ll need the ellipsoid height well as a geoid model for the local area.
What is a geoid model?
A geoid model is a location-based grid that allows you to convert between ellipsoid and a national vertical datum such as NAVD88. Geoid models are country-specific. For instance, in the United States, the current geoid model is GEOID12B.
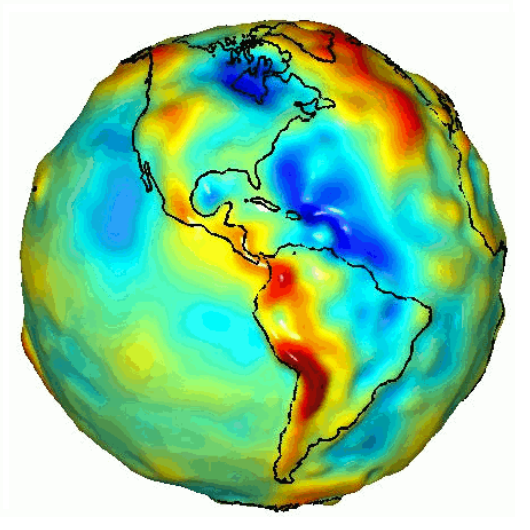
The geoid model contains an offset value called the “geoid height” or “geoid undulation.” The geoid height is a locally specific, constant number that represents the vertical difference between the reference ellipsoid and the geoid in that area. The geoid height can be positive or negative. This is the number we must use to convert between ellipsoidal and local vertical datum heights. These elevations are called the orthometric heights.
Orthometric height is the type of elevation data your surveyors, engineers, and other field workers need to work practically and accurately.
How do I convert to geoid data using the geoid model?
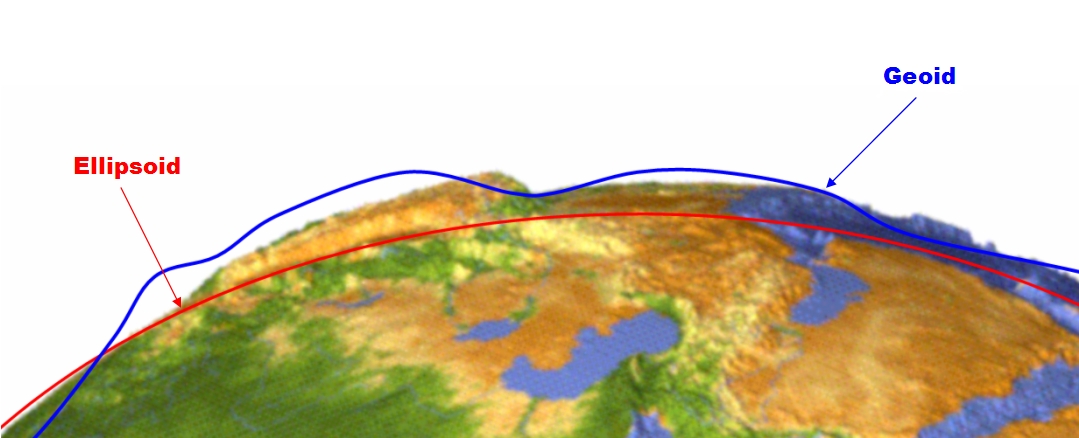
Ellipsoid and geoid difference[/caption]
Because geoid height is a mathematical offset between the ellipsoid and the geoid, it can be used to translate elevation data from one vertical reference to another. This means the geoid height provides the key to unlocking your GPS receiver’s accurate elevation data.
For most surveyors, GIS users, and others, they will want to convert the ellipsoidal data into an elevation measurement called the “orthometric height.”
What should I remember about the geoid datum?
- The vertical datum is an accurate physical representation of the earth’s surface
- A geoid model is a locally defined grid that allows conversion from ellipsoidal to orthometric heights
- A geoid height is a number within the geoid model that enables this conversion
- The orthometric height is the practical elevation that tries to describe the heights of points on the earth’s surface
Part 4: Calculating orthometric height from ellipsoidal data with the geoid height
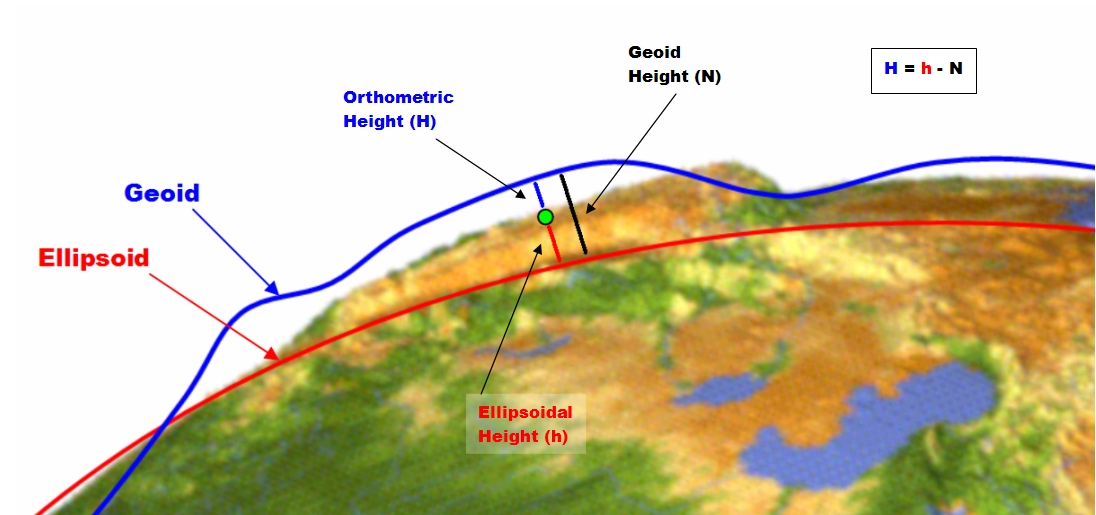
How do we use geoid height to calculate orthometric elevation? We’ll use this formula:
H = h – N
The three variables represent terms we’ve already defined. Here is what they stand for and where they come from:
| Variable: | Represents: | What it is: |
| H | Orthometric Height | This is the elevation our surveyors and field workers need |
| h | Ellipsoidal Height | This is the elevation above or below the reference ellipsoid from our GPS receiver |
| N | Geoid Height / Undulation | This is the offset between the geoid and ellipsoid references; we find N in the geoid model used |
Let’s go back to Michael Smith. Imagine Michael is validating his Arrow Gold by occupying this survey monument in Lake Oswego, Oregon. The geoid height for his location is -22.835 meters. The ellipsoidal height from his receiver is 102.451 meters. With these two figures, we can calculate the orthometric height for this survey monument. Recall our formula:
H = h – N
Where:
- H = the orthometric height we want to know
- h = 102.451 meters
- N = -22.835 meters
Therefore, our calculation is this:
H = (102.451 meters) – (-22.835 meters)
Because two negatives create a positive, we will rewrite our equation like this:
H = 102.451 meters + 22.835 meters = 125.286 meters
Now we see the orthometric height for Michael’s receiver is 125.286 meters. This is very close to the 125.2-meter value from the survey monument datasheet. (Note that the vertical confidence level of the datasheet is 95 percent, or within 2.78 cm.) Therefore, we have validated Michael’s GNSS receiver elevation data!
Michael can breathe easy and send his field crews to survey his utility assets.
What should I remember about orthometric height?
- The formula for calculating orthometric height is “H = h – N”
- You need the geoid and ellipsoidal heights to perform this conversion
Part 5: Conclusion — Final thoughts on GPS receiver elevation data
At the end of the day, every theoretical model of the earth’s surface is a conceptualized view of a changing, living, breathing surface. By combining the knowledge of more than a hundred countries’ unique geoid models with the high-accuracy capabilities of Eos Arrow technology, we hope to provide your organization with not only the tools to capture and use elevation data, but also the resources to understand what’s happening behind the scenes.
If you’d like to discover more about elevation data now, then you can view this introduction video by David Doyle for beginners.
GPS Receiver Elevation: Glossary of Terms
- Ellipsoid – A theoretical conceptualization of the earth’s surface that imagines the earth is a mathematically perfect ellipsoid
- Ellipsoidal Height – An elevation measurement taken above or below the reference ellipsoid
- Geoid– A representation of the earth’s surface based on the Earth’s gravity field which best fits a global mean sea level
- Geoid Model – A location-specific set of constants to convert between ellipsoidal and geoidal datums
- Geoid Height – A location-specific constant contained within the geoid model that is used in ellipsoidal-orthometric height conversions
- Orthometric Height – The actual elevation above or below the geoid
- Mean Sea Level (MSL) – An arithmetic average height of the sea with respect to the earth’s surface based on 19 years of tidal highs and lows
Extra: How do you find “N” for the geoid?
Big thanks to Eos newsletter reader Loren A., who let us know about this terrific computational tool from NOAA. The tool helps you find your “N” value for the geoid conversion. Thanks, Loren!
Do you have comments or feedback? Email us directly or leave a comment below! We read every comment that comes in. — Eos